www.relatedscience.com
El principio del palomar dice lo siguiente: si hay más palomas que palomares, alguno de los palomares deberá contener por lo menos dos palomas. En general, podemos hablar de objetos y cajas donde guardar estos objetos. La verdad es que es un principio tan simple que no necesita demostración.

Mostremos algunos ejemplos sencillos de aplicación de este principio a cuestiones más o menos cotidianas.
Ejemplo 1: En cualquier espectáculo del Teatro Campos Elíseos de Bilbao, que esté lleno, existen dos personas del público tales que su primera y su última letra son iguales (como por ejemplo, Aitor y Amador, o Sorkunde y Salomé).
El aforo del Teatro Campos Elíseos es de 800 personas, que van a ser
nuestras palomas, mientras que los pares formados por la primera y
última letra de un nombre (en los ejemplos anteriores (a,r), de Aitor y
Amador, y (s,e), de Sorkunde y Salomé), nuestros palomares. Puesto que
hay 27 letras en el alfabeto, entonces hay 27 x 27 = 729 pares de letras
posibles, desde la (a,a) hasta la (z,z). Como hay más palomas
(personas) que palomares (pares de letras), entonces al menos dos
personas deberán compartir la primera y la última letra de su nombre.
Ejemplo 2: En una fiesta cualquiera hay por lo menos dos personas con el mismo número de amigos.
Supongamos que a una fiesta, o reunión de cualquier tipo, han asistido n personas, bueno para que no parezca tan abstracto, pensemos que han sido 32 personas. Podríamos distinguir dos casos:
A. Si todas las personas de la reunión tienen al menos un amigo, cada
una de esas 32 personas (que van a ser ahora nuestras palomas) pueden
tener entre 1, ya que todas tienen al menos un amigo, y 31 amigos, ya
que suponemos que “cada persona no es amiga de sí misma” (las cantidades
de amigos son ahora los palomares), entonces aplicando el principio del
palomar existen dos personas con el mismo número de amigos.
B. Pero si hubiese algunas personas en la fiesta que no tienen ningún
amigo, razonaremos como antes, aunque sin tener en cuenta a las
personas “solitarias”. Por ejemplo, si de las 32 que están en la fiesta,
7 no tienen amigos, se hace el razonamiento anterior con las 25
personas restantes, que ahora pueden tener entre 1 y 24 amigos.

Ejemplo 3: Siempre que haya 9 personas en una reunión, de edades comprendidas entre 18 y 58 años, es posible elegir dos grupos de personas tal que las sumas de las edades de las personas de cada grupo sean iguales.
Como estamos buscando grupos de personas dentro del grupo total de 9
personas, es decir, subconjuntos del conjunto de nueve elementos, es
útil recordar que hay un total de 29 subconjuntos del
conjunto de 9 elementos (esta es una cuestión que no vamos a explicar
aquí hoy, pero que tiene que ver con los números combinatorios y el
binomio de Newton), incluido el vacío, luego 511 subconjuntos no vacíos.
Estos van a ser las palomas en esta ocasión.
Ahora, como las edades de las personas de la reunión están
comprendidas entre los 18 y los 58 años, las sumas de las edades de
cualquier subconjunto de personas están comprendidas entre 18 = 1 x 18
(una única persona, y que tenga la menor de las edades posibles) 522 = 9
x 58 (las nueve personas, y que todas tuviesen la mayor edad posible).
Por lo tanto, tenemos 504 valores posibles para las sumas de las edades
de las personas de cualquier subconjunto de las personas que están en
esta reunión. Estos van a ser los palomares.
En consecuencia, el principio del palomar nos dice que existen dos
subconjuntos distintos, del grupo de 9 personas que hay en la reunión,
con la misma suma de las edades de las personas de cada uno de ellos.
Pero podría ocurrir que en esta conclusión, consecuencia del
principio de Dirichlet, hubiese alguna persona que estuviese siendo
considerada a la vez en esos dos subconjuntos que existen. Si esto
ocurriese, no tenemos más que eliminar a esa persona de cada uno de los
dos subconjuntos, y los dos nuevos subconjuntos que obtenemos siguen
cumpliendo la propiedad de que la suma de las edades de sus miembros es
la misma, ya que al eliminar a la misma persona de ambos, se quita el
mismo número a las sumas de las edades, y se sigue manteniendo la
igualdad.
Aunque estamos poniendo ejemplos más bien cotidianos para entender la
fuerza del principio, lo interesante es que se puede aplicar a todo
tipo de situaciones, de hecho, como decíamos al principio, es una
potente herramienta en matemáticas.
El primer matemático en utilizarlo explícitamente dentro de su investigación fue el matemático prusiano Gustav L. Dirichlet (1805-1859),
para demostrar un resultado de aproximación de números irracionales
mediante racionales (recordemos que los números racionales son aquellos
que se pueden expresar como división de dos números enteros, por
ejemplo, 5/2, y que si los expresamos con decimales o tienen un número
finito de decimales, o un número finito que se repite periódicamente),
por este motivo se conoce también como el principio de Dirichlet.
En particular, se pueden demostrar muchos resultados de teoría de
números haciendo uso del principio del palomar. A continuación,
mostramos algunos sencillos ejemplos.
Ejemplo 4: Consideremos un conjunto arbitrario de 47 números, entonces existen al menos dos cuya diferencia es divisible por 46.
Antes de explicar la aplicación del principio de Dirichlet para
probar esta afirmación, aclaremos una vez más, que esos 47 números son
arbitrarios, el resultado va a ser válido cualesquiera que sean los 47
números que se consideren.
¿Cómo utilizar el principio para demostrar este resultado? Cuando
dividimos un número cualquiera entre otro, en este caso nos interesa
dividir por 46, entonces obtenemos el divisor y el resto. Así, si
dividimos el número 357 entre 46 nos da 7 (el dividendo), pero nos
sobran 35 (que es el resto). Por lo tanto, 357 = 46 x 7 + 35. En matemáticas, se dice que 357 es congruente con 35, módulo 46, y se expresa  .
.
Para aplicar el principio del palomar, vamos a distribuir nuestras
palomas (que serán los 47 números arbitrarios que se han tomado) en los
siguientes 46 palomares…
P1 = conjunto de números tales que al dividir por 46 queda de resto 0 (es decir, los números congruentes con 0, módulo 46),
P2 = conjunto de números tales que al dividir por 46 queda de resto 1 (es decir, los números congruentes con 1, módulo 46),
…
P46 = conjunto de números tales que al dividir por 46 queda de resto 45 es decir, los números congruentes con 45, módulo 46).
En consecuencia, habrá por lo menos dos palomas, es decir, dos
números del conjunto de 47 que habíamos elegido arbitrariamente,
compartiendo palomar, es decir, que tienen el mismo resto al dividir por
46.
Esos dos números se podrán escribir, como antes hemos hecho con el
número 357, de la forma, 357 = 46 x 7 + 35, con distintos divisores,
pero el mismo resto. Al restar ambos números, como los dos tienen el
mismo resto, el resultado quedará múltiplo de 46, y se concluye el
resultado.
Ejemplo 5: Sean a1, a2, …, a100 cien números enteros (es decir, pueden ser positivos, negativos o cero), distintos o no (esto es, puede aparecer un mismo número más de una vez) , cualesquiera. Entonces, existen dos números r y s, contales que la suma
es un múltiplo de 100.
Aunque es una afirmación bastante sorprendente, realmente el
argumento es muy similar al anterior. Para cada número t, entre 1 y 100,
consideramos la suma parcial 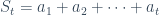 y el resto
y el resto  de dividir
de dividir  entre 100.
entre 100.
Si alguno de los  es cero, entonces la suma correspondiente
es cero, entonces la suma correspondiente 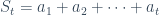 es múltiplo de 100, y se satisface el resultado deseado. En otro caso,
para los t entre 1 y 100 (que serán nuestras paloma), los restos
es múltiplo de 100, y se satisface el resultado deseado. En otro caso,
para los t entre 1 y 100 (que serán nuestras paloma), los restos 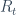 toman valores entre 1 y 99 (que serán nuestros palomares), de donde se deduce que habrá dos de los términos
toman valores entre 1 y 99 (que serán nuestros palomares), de donde se deduce que habrá dos de los términos 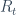 iguales. Es decir, existen r y s con
iguales. Es decir, existen r y s con 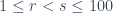 , tal que
, tal que  . Es decir, al dividir
. Es decir, al dividir 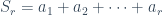 y
y 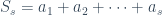 entre 100, se obtiene el mismo resto. Luego
entre 100, se obtiene el mismo resto. Luego  es múltiplo de 100, esto es,
es múltiplo de 100, esto es,  es múltiplo de 100.
es múltiplo de 100.
Por supuesto, que aquí el número 100 no es especial, y el resultado será válido para otros números.
Ejemplo 6: Si se toman n+1 números cualesquiera del conjunto {1, 2, …, 2n}, al menos habrá entre ellos dos elementos x e y tal que x divide a y.
Este problema apareció en la Competición Putnam (Competición
Matemática William Lowell Putnam), que es una competición en Estados
Unidos y Canadá de problemas de matemáticas para estudiantes de colleges
universitarios, de 1958.
Según parece la demostración que vamos a mostrar de este resultado se
debe a los matemáticos húngaros Paul Erdös (1913-1996) y Georges
Szekeres (1911-2005). La idea para demostrar la anterior afirmación es
dividir el conjunto de los 2n primeros números {1, 2, …, 2n} en n
conjuntos T1, T2, …, Tn, de forma que
si se cogiesen n+1 números del conjunto {1, 2, …, 2n}, por el principio
de Dirichlet, al menos dos de ellos deberían estar en un mismo conjunto Ti.
Por lo tanto, si estos conjuntos Ti tuviesen la propiedad de que para cualesquiera elementos x < y de un mismo conjunto, entonces x divide a y (se denota x | y), se habría concluido la demostración. En consecuencia, para poder concluir el resultado, los conjuntos Ti deberán estar formados por elementos {x1, x2, …, xn} tales que sus elementos se dividen unos a otros, x1 | x2 | …| xn. Para ello, se definen los conjuntos T1, T2, …, Tn, como la intersección del conjunto {1, 2, …, 2n} con los siguientes conjuntos
{1, 2, 22, 23,…}, {3, 3 x 2, 3 x 22, 3 x 23,…}, {5, 5 x 2, 5 x 22, 5 x 23,…}, etc,
que verifican la propiedad de divisibilidad anterior, cada elemento
divide al siguiente en el conjunto, y además, cada número del conjunto
inicial {1, 2, …, 2n} puede escribirse de forma única como (2m – 1) x 2k, luego pertenece a uno de esos conjuntos. Es decir, acabamos de dividir el conjunto {1, 2, …, 2n} en n conjuntos T1, T2, …, Tn, con la propiedad adecuada, y el resultado queda demostrado.

También se pueden demostrar resultados geométricos. En esta entrada del Cuaderno de Cultura Científica mostraremos un ejemplo sencillo.
Ejemplo 7: Dados 5 puntos cualesquiera dentro de un triángulo equilátero (luego con los tres lados iguales) de lado 2, al menos dos de ellos están a una distancia, el uno del otro, menor que 1.
Está claro que por estar dentro de un triángulo equilátero de lado 2,
cualesquiera dos puntos, de los cinco que hemos elegido, están a una
distancia menor que 2, pero ¿podemos afirmar que siempre habrá dos de
ellos que estén a una distancia menor que 1?
Para aplicar el principio de Dirichlet se consideran los puntos
medios de los lados del triángulo y se unen con segmentos, lo cual
divide al triángulo en cuatro triangulitos equiláteros de lado 1. Como
son cuatro triángulos de lado 1 (que serán nuestros palomares) y cinco
puntos (que serán nuestras palomas), entonces habrá dos puntos en el
mismo triángulo equilátero de lado 1, y esos dos están a una distancia
menor que 1.

Para finalizar, existe una versión generalizada del principio del palomar,
que viene a decirnos que si hay muchas más palomas que palomares, vamos
a poder afirmar que algún palomar tiene bastantes más de dos palomas.
En concreto, dice que si hay n palomas y k palomares (n > k), existe
al menos un palomar con al menos (no solo dos, sino) n/k palomas, es
decir, el valor máximo es al menos mayor que el valor medio. Así, en la
Behobia-San Sebastián de 2014 había al menos 84 personas que cumplen
años el mismo día. Las personas que participaron en la carrera
Behobia-San Sebastián de 2014, que son ahora las palomas, eran 30.701 y
cada día del año son los palomares, 366. Entonces, como 30.701/366 =
83,88, se obtiene el resultado.
En mi siguiente entrada del Cuaderno de Cultura Científica
volveremos a la carga con más ejemplos de aplicaciones del principio del
Palomar, algunos más cotidianos, otros de teoría de números y algunos
geométricos, y entre ellos estará la demostración de Dirichlet para
aproximar los números irracionales con números racionales.

Por cierto, no quisiera terminar esta entrada sin comentaros que el
principio de Dirichlet es tan potente, que he conseguido demostrar,
utilizando esta herramienta matemática, nada más y nada menos que la
hipótesis de Riemann… pero visto que hemos llegado al final de la entrada, os dejo la prueba de este resultado como ejercicio.
Bibliografía
1.- Dimitri Fomin, Sergey Genkin, Ilia Itenberg, Círculos matemáticos, Biblioteca de Estímulos Matemáticos, SM-RSME, 2012.
2.- R. B. J. T. Allenby, Alan Slomson, How to count, an introduction to combinatorics, CRC Press, 2011.
Por César Tomé
Sobre el autor: Raúl Ibáñez es profesor del Departamento de Matemáticas de la UPV/EHU y colaborador de la Cátedra de Cultura Científica



No hay comentarios:
Publicar un comentario